单纯形算法

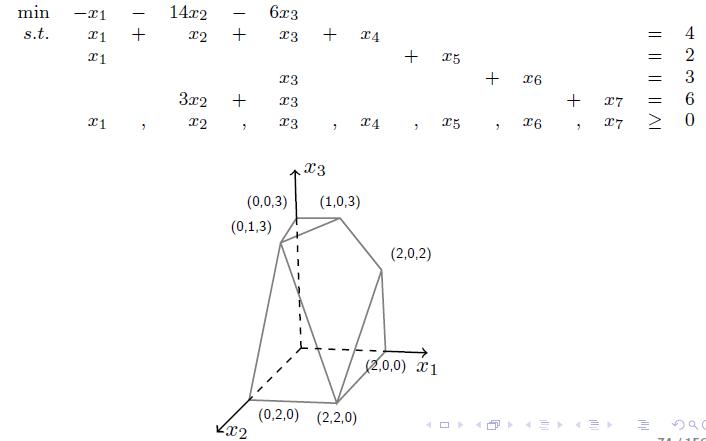
中学课程里，我们都简单地接触过线性规划，那时候一般都是分析每个约束，在二维平面上画出直线，得到可行域，然后以固定斜率作出目标函数直线，在可行域内移动直线，在y轴上的截距就是最优解。而往往最优解的地方是通过（凸）可行域的顶点。就像下面这个例子： $$ \begin{equation} \begin{split} \max& \quad x_3+x_4\cr s.t.& \quad -x_3+2x_4\leq 2 \cr &\quad 3x_3-2x_4\leq 6 \cr &\quad x_3, x_4\geq 0 \end{split} \end{equation} $$

蓝色区域是可行域，红色直线是固定斜率的，当上移到（4，3）点时目标函数取最大值。

而我们后面将证明，最优解一定是可行域（凸超几何体）的顶点之一。那么，我们先假定这成立，就使用”改进-停止“（improve-stopping）的套路，即给定可行域的一个顶点，求值，沿一条边到达下一个顶点，看是否能改善解，直到达到停止要求。

这里就要问几个问题了：为什么最优解一定在顶点处？怎么得到顶点？怎么实现沿着一条边到下一个顶点？什么时候停止？接下来，我们将一一解答这些问题，当解答完这些问题，单纯形法也就显而易见了。

1 凸多边形最优解在顶点

考虑最小化问题，目标函数$\mathbf{c}^T \mathbf{x}$，有一个在可行域内部的最优解$\mathbf{x}^{(0)}$，因为凸多边形内部任一点都可以表示成顶点的线性组合，即对于顶点$\mathbf{x}^{(k)}, k=1,2,\cdots, n$，有 $$ \mathbf{x}^{(0)}=\sum_{k=1}^{n}\lambda_k\mathbf{x}^{(k)}, $$

$$ \sum_{k=1}^n \lambda_k=1 $$

假设$\mathbf{x}^{(i)}$是所有顶点中使得$\mathbf{c}^T \mathbf{x}$最小的顶点，那么有 $$ \begin{equation} \begin{split} \mathbf{c}^T\mathbf{x}^{(0)} &= \sum_{k=1}^{n}\lambda_k\mathbf{c}^T\mathbf{x}^{(k)} \cr &\geq \sum_{k=1}^{n}\lambda_k\mathbf{c}^T\mathbf{x}^{(i)} \cr &= \mathbf{c}^T\mathbf{x}^{(i)} \end{split} \end{equation} $$

因此，总有一个顶点，他的目标函数值不比内部点差。

2 怎样得到一个凸多边形的顶点？

下面要说明的就是这样一个定理：对于可行域方程组$\mathbf{Ax=b}​$，该方程确定的凸多边形的任意一个顶点对应$\mathbf{A}​$的一组基。

2.1 顶点对应一组基

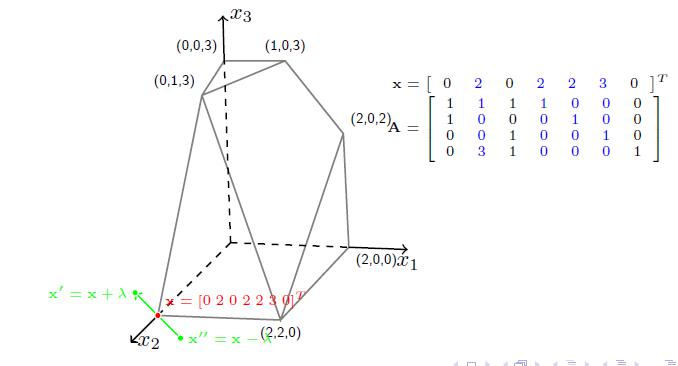
上面这个例子是松弛形式的约束，原来的变量有三个，加上后面4个后变成等式，形成的可行域如上图所示。我们取一个顶点（0，2，0）分析，代入约束中，可以算出一个完整解$x=(0，2，0，2，2，3，0)$。取出矩阵$\mathbf{A}$中对应的$x$不为0的列，即图中标蓝的几列（用$\mathbf{a}_2$，$\mathbf{a}_4$，$\mathbf{a}_5$，$\mathbf{a}_6$表示），那么这几列就是线线性无关的，考虑$m<n$（约束数目小于松弛后的变量个数），那么自由解有$n-m$维，因此挑出来的列必有$m$个，构成一组基。下面主要说明他们为什么线性无关。假设他们线性相关，即存在一组$\lambda\neq\mathbf{0}$，使得$\lambda_2\mathbf{a}_2+\lambda_4\mathbf{a}_4+\lambda_5\mathbf{a}_5+\lambda_6\mathbf{a}_6=0$，也就是说，可以构造$\lambda=[0, \lambda_2, 0, \lambda_4, \lambda_5, \lambda_6, 0]$，使得$\mathbf{A}\lambda=0$。那么还可以再构造两个异于$x$的解：$x’=x+\theta\lambda$和$x^{’’}=x-\theta\lambda$。他们都满足$\mathbf{Ax=b}$。并且可以通过控制$\theta$取很小的正值，使得这两个解满足都大于0的约束。由此这两个解都在凸多面体内，并且有$x=\frac{1}{2}(x’+x^{’’})$，但是这是有问题的，因为一个凸多面体的顶点是不能被内部点线性表示的，因此这几列是构成一组基的。

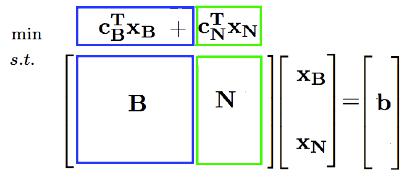
在这里，我们还可以对每一组解，都将$\mathbf{A}​$的列重新排列一下，将解向量也排列一下，写成分块矩阵的形式，那么就会有$\mathbf{x}_\mathbf{B}=\mathbf{B}^{-1}\mathbf{b}​$和$ \mathbf{c}^T \mathbf{x}= \mathbf{c}^T_{\mathbf{B}}\mathbf{B}^{-1}\mathbf{b}​$。这是两个很有用的式子，在后面单纯形算法的理解上很有帮助，这里先记下。

2.2 一组基对应一个基可行解（顶点）

有了上面的知识，给定一组基$\mathbf{B}​$，我们直接构造$\mathbf{x}=[\mathbf{B^{-1}b}, \mathbf{0}]^T​$，只要说明他不能被两个异于他的内部点线性表示即可。假设有两个内部点$\mathbf{x}_{1}​$和$\mathbf{x}_2​$，满足$\mathbf{x}=\lambda_1\mathbf{x}_1+\lambda_2\mathbf{x}_2​$，由于$\mathbf{x_N}=0​$，并且这些解的元素都大于等于0，因此$\mathbf{x}_{1\mathbf{N}}=\mathbf{x}_{2\mathbf{N}}=0​$。而又因为$\mathbf{Ax_1=Ax_2=b}​$，因此$\mathbf{x}_{1\mathbf{B}}=\mathbf{x}_{2\mathbf{B}}=\mathbf{B^{-1}b}​$。即这两个解和$\mathbf{x}​$相同，因此$\mathbf{x}​$是顶点。

3 如何从一个顶点沿着边到另一个顶点？

这里是要研究怎么改善一个解，我们需要知道怎么从一个顶点出发沿着边找到另一个顶点。前面我们知道了一个顶点对应一组基，而且一个矩阵的基有多个，那么是否可以通过基的变换从而使得顶点变换呢？先来看一个例子。

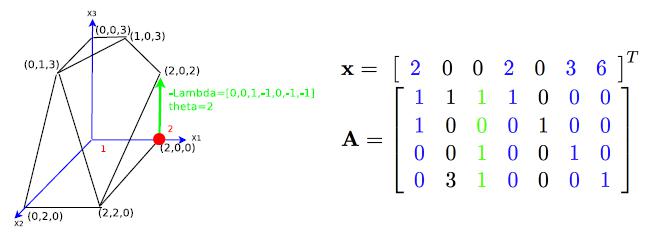
图中红色点对应一个完全解$\mathbf{x}=[2,0,0,2,0,3,6]$，对应的基是$\mathbf{B}=\{\mathbf{a}_1，\mathbf{a}_4，\mathbf{a}_6，\mathbf{a}_7\}$，考虑向量$\mathbf{a}_3$，即绿色那列，他可以表示成： $$ \mathbf{a}_3=0\mathbf{a}_1+1\mathbf{a}_4+1\mathbf{a}_6+1\mathbf{a}_7 $$

将式子补全，就会有 $$ 0\mathbf{a}_1+0\mathbf{a}_2-1\mathbf{a}_3+1\mathbf{a}_4++0\mathbf{a}_5+1\mathbf{a}_6+1\mathbf{a}_7=0 $$ 把系数写出来：$\lambda=[0,0,-1,1,0,1,1]$，他就是对应上图中的绿色向量（相反方向）。因此，只有沿着这个方向走适合的步长$\theta$，就能到达下一个顶点。即新的顶点和旧的顶点关系为： $$ \mathbf{x’}=\mathbf{x}-\theta\mathbf{\lambda}(\theta>0) $$

那么多大的$\theta$合适呢？我们很容易知道$\mathbf{x’}$能够满足$\mathbf{Ax=b}$，因为$\mathbf{A\lambda=0}$，现在要保证的就是$\mathbf{x’}$的各个分量大于等于0。对于$\lambda_i\leq0$的项，相减后大于0，没问题。但是对于$\lambda_i>0$的项，就要小心了，为了保证相减后仍然大于等于0，我们设置 $$ \theta=\min\limits_{\mathbf{a}_i\in \mathbf{B},\lambda_i>0}\frac{x_i}{\lambda_i} $$

就能保证$\mathbf{x’}\geq0$。在上面的例子中，$\theta=2$，新解是$\mathbf{x’}=[2,0,2,0,0,1,4]$，对应的基是$\mathbf{B’}=\{\mathbf{a}_1，\mathbf{a}_3，\mathbf{a}_6，\mathbf{a}_7\}$，到这里，一切看上去很完美，我们找到了运动到下一个顶点的方法，也就是先找一个非基向量，将他写成用基向量表示的形式，提出系数，确定步长，得到新解。但是还有一个小问题，我们看到实际上$\mathbf{B’}$和$\mathbf{B}$差了一个向量，相当于把$\mathbf{a_4}$换出去，把$\mathbf{a}_3$换进来。我们称这个过程为换基，后面算法实现部分叫pivot。那么，怎么保证换了个向量之后，仍然是基呢？证明一下：

证明：$\mathbf{B’}=\mathbf{B}-{\mathbf{a}_l}+{\mathbf{a}_e}$仍然是基。（$l$表示leave，$e$表示enter）

假设$\mathbf{B’}$线性相关，那么存在$<d_1,d_2,\ldots,d_{l-1},d_{l+1},\ldots,d_m, d_e> \neq 0$，使得$\sum_{k}d_k\mathbf{a}_k=0$。而$\mathbf{a}_e=\sum_{i=1}^m \lambda_i\mathbf{a_i}$，代入得： $$ (d_1+d_e\lambda_1)\mathbf{a_1}+\ldots+(d_e\lambda_l)\mathbf{a}_l+\ldots+(d_m+d_e\lambda_m)\mathbf{a}_m=0 $$

这里是证明的关键之处：我们在设置$\theta$时的做法，假如最终选出来的使得$\frac{x_i}{\lambda_i}$最小的那一项下标为$p$，那么得到的新解的第$p$项必然为0，相当于把$\mathbf{a}_p$换了出去。在上面这个例子中$p=4$。而因为我们只考虑$\lambda_i>0$的基向量，因此被换出去的基$\mathbf{a}_l$对应的$\lambda_l>0$，因此上式中有$d_1=d_2=\ldots=d_m=d_e=0$，和原假设矛盾，因此$\mathbf{B’}$也是线性无关的。

截止到目前，我们回答了三个问题，基本上单纯形算法呼之欲出了，单纯形算法就是通过反复的基变换（通过向量的进出）来找顶点，从而找到达到最优值的顶点。但是还是有些细节需要琢磨，比如，怎么选入基向量？改善的过程什么时候停止？

4 入基向量的选择及停止准则

以最小化问题为标准，我们的最终目标是最小化$\mathbf{c^Tx}$，因此一个很自然的贪心想法是每步的改善都尽可能地大，因此可以计算一下更新的目标函数值和原来的差值，取使得变化大的顶点继续下一步迭代。那么这个差值怎么能够向量化地计算呢？只有向量化地计算，才能避免一个一个地计算比较，提高效率。

假设$\mathbf{B}=\{\mathbf{a}_1, \mathbf{a}_2,\ldots, \mathbf{a}_m\}​$，那么对于任何一个非基向量$\mathbf{a}_e​$，都有$\mathbf{a}_e=\lambda_1\mathbf{a}_1+\ldots+\lambda_m\mathbf{a}_m​$。将$\lambda​$写完整：$\lambda=[\lambda_1,\lambda_2,\ldots,\lambda_m,0,0,\ldots,-1,\ldots,0]^T​$，差值 $$ \mathbf{c}^T\mathbf{x}’-\mathbf{c}^T\mathbf{x}=\mathbf{c}^T(-\theta\lambda)=\theta(\mathbf{c}_e-\sum_{\mathbf{a}_i\in B}\lambda_i\mathbf{c}_i) $$

因此我们要选使得这个值的绝对值最大的$\mathbf{a}_e​$。那么什么时候表示找到最优值应该停止呢？很明显，就是对于所有$\mathbf{a}_e​$，这个差值都大于等于0，即目标函数不再减小。因此，每次迭代，先计算差值，如果存在小于0的，就选一个使得差值绝对值最大的作为入基向量。

嗯，接下来就是要考虑向量化操作。首先我们看一下$\lambda$能不能向量化表示：由于$\mathbf{B}\lambda=\mathbf{a}_e$（$\lambda$只取基系数部分），因此$\lambda=\mathbf{B^{-1}}\mathbf{a}_e$，如果对整个矩阵$\mathbf{A}$左乘$\mathbf{B^{-1}}$，这就很有意思了，所有的非基列将变成该非基向量用基向量表示的系数，而所有的基列将变成$e_k$，即合起来成为一个单位阵的形式。这是很关键的一步，在单纯形算法实现中也涉及到，先记下。进一步，我们取$\mathbf{c}$的基部分$\mathbf{c_B}$，这样$\mathbf{c}_\mathbf{B}^T\mathbf{B}^{-1}\mathbf{A}$就等于了上式中的$\sum*_{\mathbf{a}_i\in \mathbf{B}}\lambda_i\mathbf{c}i$的向量化形式（对所有的非基向量一同操作）。然后再加上一部分，变成$\mathbf{c}^T-\mathbf{c}_\mathbf{B}^T\mathbf{B}^{-1}\mathbf{A}$，这就是最终的形式，称之为检验数$\bar{\mathbf{c}}$。很容易验证，基向量对应的检验数都是0，我们的目标就是通过迭代，使得$\bar{\mathbf{c}}\geq0$，这时对于任何一个可行解$\mathbf{y}$（$\mathbf{Ay=b,y\geq0}$），都有$\mathbf{c}^T\mathbf{y}\geq\mathbf{c}_\mathbf{B}^T\mathbf{B}^{-1}\mathbf{A}\mathbf{y}=\mathbf{c}\mathbf{B}^T\mathbf{B}^{-1}\mathbf{b}=\mathbf{c}_\mathbf{B}^T\mathbf{x}_\mathbf{B}=\mathbf{c}^T\mathbf{x}$，即$\mathbf{x}$就是最优的。

5 单纯性算法核心：单纯形表

终于，一系列的讲解结束，单纯性算法也就顺理成章了。要将上面的一堆东西整理成一个简短高效的可行算法并不简单。先贴上算法伪代码：

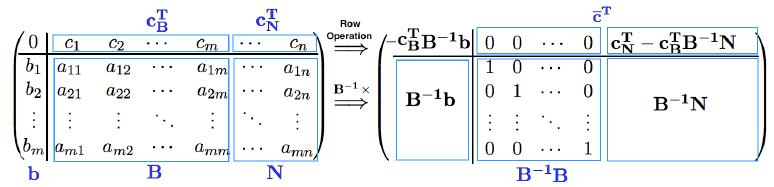
再献上一个非常漂亮的单纯形表：

现在，我们来对算法进行分析，将算法的每个操作和我们上面的介绍对应起来。

• SIMPLEX算法一开始调用INITIALIZESIMPLEX找到一个初始基可行解，这在某些情况下很简单，当$\mathbf{b}\geq0$时，他就是一个初始基可行解，否则，可能要用到两阶段法、大M法等求，这不是重点。

• WHILE循环内，只要找到一个$c_e<0$，就继续迭代。第10到16行就是通过设定$\theta$找到出基向量。

• 最关键最有意思的就是PIVOT算法，他巧妙地将我们介绍的繁杂操作使用一个简单的高斯行变换就实现了。而这个算法的载体就是单纯形表，如上图，左上角是目标函数值相反数$-z$，第一行是检验数$\bar{\mathbf{c}}$，左下角是基对应的部分解（其他部分是0，不用写出），右下角是矩阵$\mathbf{A}$。他始终被分块成两部分，基向量部分始终以单位阵的形式存在。注意左边的部分解每个分量都是严格对应着一个基向量，即他们是有顺序的。

• 一行一行地看PIVOT算法。输入参数告诉我们下标为$l​$的向量被换出，因此找到他对应的那行，暂称为第$l​$行，这一行对应的基的下标要被换成$e​$，那么为什么更新后对应的解是$\frac{b_l}{a_{le}}​$呢，要注意，其实这个值就是$\theta​$，$b_l​$就是旧的$x_i​$，$a_{le}​$就是$\lambda_i​$（上面已经解释了乘上$\mathbf{B^{-1}}​$后每一列都是系数）。那么为什么更新后是$\theta​$呢？我们回到式子$\mathbf{x’=x-\theta\lambda}​$，由于$b_l​$现在对应的新向量不是$\mathbf{x}​$对应的基向量，因此$\mathbf{x}​$在该位置的值是0，而我们知道$\lambda​$在入基向量对应的位置的值是-1，因此$0-(-1)\theta=\theta​$。

• 第3到4行，将第$l$行除以$a_{le}$，目的就是将$a_{le}$变成1，因为要始终保持基是以单位阵的形式存在。

• 第8行，就是在执行$\mathbf{x’=x-\theta\lambda}$的操作，得到新解。

• 第10行，高斯行变换，你会发现这样操作完后，入基列就变成和刚才出基列一样，高斯行变换保证了矩阵的性质。

• 第14行，我们知道$-z=0-\mathbf{c}_\mathbf{B}^T\mathbf{B}^{-1}\mathbf{b}​$，由于旧有的基对应的$c​$都是0，而只有新换入的向量对应的$c_e​$不为0，具体写一下，减掉的那部分就只有$c_e​$和他对应的解$b_l​$的乘积了。同理，第16行，$\mathbf{c}^T-\mathbf{c}_\mathbf{B}^T\mathbf{B}^{-1}\mathbf{A}​$，由于也是只有$c_e​$不为0，因此就和他对应的$\mathbf{A}​$的第$l​$行相乘了。

到此，终于介绍完了单纯形算法。其他还有一些要注意的地方，比如一定要注意检验数和原目标函数的$\mathbf{c}​$是完全不一样的概念，在原约束为不等式，需要加松弛变量的情况下，他们可能相等，但心里一定要区分它们，同时，这种情况下，基很容易找，就是松弛变量的那几列构成的单位阵。但是如果原约束是等式，就需要自己找基，并且这时检验数往往就和目标函数参数不同了。

最后，本文所用的截图均来自中科院计算所B老师的课程PPT，本人在学习该课程时也受益良多，对单纯形算法也钻研了比较长的时间，因此撰写本文，希望给大家一个学习参考！其中可能有错误之处，欢迎指正讨论。